Health Articles

 

Untitled

IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 On the Maximum Achievable Sum-Rate With Successive Decoding in Interference ChannelsYue Zhao, Member, IEEE, Chee Wei Tan, Member, IEEE, A. Salman Avestimehr, Member, IEEE, Suhas N. Diggavi, Member, IEEE, and Gregory J. Pottie, Fellow, IEEE Abstract—In this paper, we investigate the maximum achievable
sum-rate of the two-user Gaussian interference channel with
Gaussian superposition coding and successive decoding. We first
examine an approximate deterministic formulation of the problem,
and introduce the complementarity conditions that capture the use
of Gaussian coding and successive decoding. In the deterministic
channel problem, we find the constrained sum-capacity and its
achievable schemes with the minimum number of messages, first
in symmetric channels, and then in general asymmetric channels.
We show that the constrained sum-capacity oscillates as a function
Fig. 1. Two-user Gaussian interference channel.
of the cross link gain parameters between the information theo-
retic sum-capacity and the sum-capacity with interference treated
as noise. Furthermore, we show that if the number of messages
of either of the two users is fewer than the minimum number
required to achieve the constrained sum-capacity, the maximum
achievable sum-rate drops to that with interference treated as
user Gaussian interference channels (cf. under noise. We provide two algorithms to translate the optimal schemes
the constraints of successive decoding. While the information in the deterministic channel model to the Gaussian channel model.
theoretic capacity region of the Gaussian interference channel is We also derive two upper bounds on the maximum achievable
sum-rate of the Gaussian Han-Kobayashi schemes, which auto-
still not known, it has been shown that a Han-Kobayashi scheme matically upper bound the maximum achievable sum-rate using
with random Gaussian codewords can achieve within 1 bit/s/Hz successive decoding of Gaussian codewords. Numerical evalua-
of the capacity region and hence within 2 bits/s/Hz of the tions show that, similar to the deterministic channel results, the
sum-capacity. In this Gaussian Han-Kobayashi scheme, each maximum achievable sum-rate with successive decoding in the
user first decodes both users' common messages jointly, and Gaussian channels oscillates between that with Han-Kobayashi
schemes and that with single message schemes.
then decodes its own private message. In comparison, the sim-plest commonly studied decoding constraint is that each user Index Terms—Deterministic channel model, Gaussian interfer-
treats the interference from the other users as noise, i.e., without ence channel, successive decoding, sum-rate maximization.
any decoding attempt. Using Gaussian codewords, the corre-sponding constrained sum-rate maximization problem can be Manuscript received March 26, 2011; revised December 23, 2011; accepted formulated as a nonconvex optimization of power allocation, January 24, 2012. Date of publication March 06, 2012; date of current version which has an analytical solution in the two-user case It May 15, 2012. The work of C. W. Tan was supported by grants from the Re-search Grants Council of Hong Kong, Project No. RGC CityU 112909, and has also been shown that within a certain range of channel pa- Qualcomm Inc. The work of A. S. Avestimehr was supported in part by the NSF rameters for weak interference channels, treating interference as CAREER Award 0953117, NSF CCF1144000 grant, and by the AFOSR Young noise achieves the information theoretic sum-capacity Investigator Program Award FA9550-11-1-0064. The work of S. N. Diggaviwas supported in part by AFOSR MURI: "Information Dynamics as Founda- For general interference channels with more than two users, tion for Network Management", AFOSR MURI prime award FA9550-09-064, there is so far neither a near optimal solution information theo- subcontract to UCLA from Princeton University and by the NSF-CPS program retically, nor a polynomial time algorithm that finds a near op- by Grant 1136174. This paper was presented in part at the 2011 IEEE Interna-tional Symposium on Information Theory.
timal solution with interference treated as noise Y. Zhao was with the Department of Electrical Engineering, University of In this paper, we consider a decoding constraint—successive California, Los Angeles (UCLA), Los Angeles, CA 90095 USA. He is now with decoding of Gaussian superposition codewords—that bridges the Department of Electrical Engineering, Stanford University, Stanford, CA94305 USA. He is also with the Department of Electrical Engineering, Princeton the complexity between joint decoding (e.g., in Han-Kobayashi University, Princeton, NJ 08544 USA (e-mail: [email protected]).
schemes) and treating interference as noise. We investigate C. W. Tan is with the Department of Computer Science, City University of the maximum achievable sum-rate and its achievable schemes.
Hong Kong, Kowloon, Hong Kong (e-mail: [email protected]).
A. S. Avestimehr is with the School of Electrical and Computer Engineering, Compared to treating interference as noise, allowing successive Cornell University, Ithaca, NY 14853 USA (e-mail: [email protected].
cancellation yields a much more complex problem structure.
To clarify and capture the key aspects of the problem, we resort S. N. Diggavi and G. J. Pottie are with the Department of Electrical En- gineering, University of California, Los Angeles (UCLA), Los Angeles, CA to the deterministic channel model In the information 90095 USA (e-mail: [email protected]; [email protected]).
theoretic capacity region for the two-user deterministic interfer- Communicated by S. Jafar, Associate Editor for Communication Networks.
ence channel is derived as a special case of the El Gamal-Costa Color versions of one or more of the figures in this paper are available online deterministic model and is shown to be achievable using Digital Object Identifier 10.1109/TIT.2012.2190040 0018-9448/$31.00 2012 IEEE ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE We transmit messages using a superposition of Gaussian code- are constant complex channel gains, books, and use successive decoding. To capture the use of succes- is the transmitted signal of the encoded messages from the th sive decoding of Gaussian codewords, in the deterministic for- mulation, we introduce the complementarity conditions on the There is an average power constraint equal to bit levels, which have also been characterized using a conflict . In the following, we first formulate the problem graph model in We develop transmission schemes on the of finding the sum-rate optimal Gaussian superposition coding bit-levels, which in the Gaussian model corresponds to message and successive decoding scheme, and then provide an illustra- splitting and power allocation of the messages. We then derive tive example to show that successive decoding schemes do not the constrained sum-capacity for the deterministic channel, and necessarily achieve the same maximum achievable sum-rate as show that it oscillates (as a function of the cross link gain pa- rameters) between the information theoretic sum-capacity andthe sum-capacity with interference treated as noise. Furthermore, A. Gaussian Superposition Coding and Successive Decoding: the minimum number of messages needed to achieve the con- A Power and Decoding Order Optimization strained sum-capacity is obtained. Interestingly, we show that Suppose the th user uses a superposition of if the number of messages is limited to even one less than this the information rate of mes- minimum capacity achieving number, the maximum achievable . For the th user, the transmit signal sum-rate drops to that with interference treated as noise.
We then translate the optimal schemes in the determin- has a block length , and is chosen from a codebook of size istic channel to the Gaussian channel, using a rate constraintequalization technique. To evaluate the optimality of the trans- that encodes message , generated using independent lated achievable schemes, we derive and compute two upper and identically distributed (i.i.d.) random variables of bounds on the maximum achievable sum-rate of Gaussian With the power constraints Han-Kobayashi Since a scheme using superpositioncoding with Gaussian codebooks and successive decoding isa special case of Han-Kobayashi schemes, these bounds auto-matically apply to the maximum achievable sum-rate with suchsuccessive decoding schemes as well. We select two mutually exclusive subsets of the inequality constraints that characterizethe Gaussian Han-Kobayashi capacity region. Maximizing thesum-rate with each of the two subsets of inequalities leads to one is the power allocated to message of the two upper bounds. The two bounds are shown to be tight The th receiver attempts to decode all in different ranges of parameters. Numerical evaluations show using successive decoding as follows. It chooses a decoding that the maximum achievable sum-rate with Gaussian superposi- messages from both users. It starts tion coding and successive decoding oscillates between that with decoding from the first message in this order (by treating all Han-Kobayashi schemes and that with single message schemes.
other messages that are not yet decoded as noise,) then peeling The remainder of the paper is organized as follows. it off and moving to the next one, until it decodes all the mes- formulates the problem of sum-rate maximization with suc- sages intended for itself— cessive decoding of Gaussian superposition codewords in Denote the message that has order Gaussian interference channels, and compares it with Gaussian th message of the th user. Then, for the successive Han-Kobayashi schemes. reformulates the problem decoding procedure to have a vanishing error probability as the with the deterministic channel model, and then solves for the , we have the following constraints on the constrained sum-capacity. translates the optimal rates of the messages: schemes in the deterministic channel back to the Gaussianchannel, and derives two upper bounds on the maximumachievable sum-rate. Numerical evaluations of the achievabilityagainst the upper bounds are provided. concludesthe paper with a short discussion on generalizations of the coding-decoding assumptions and their implications.
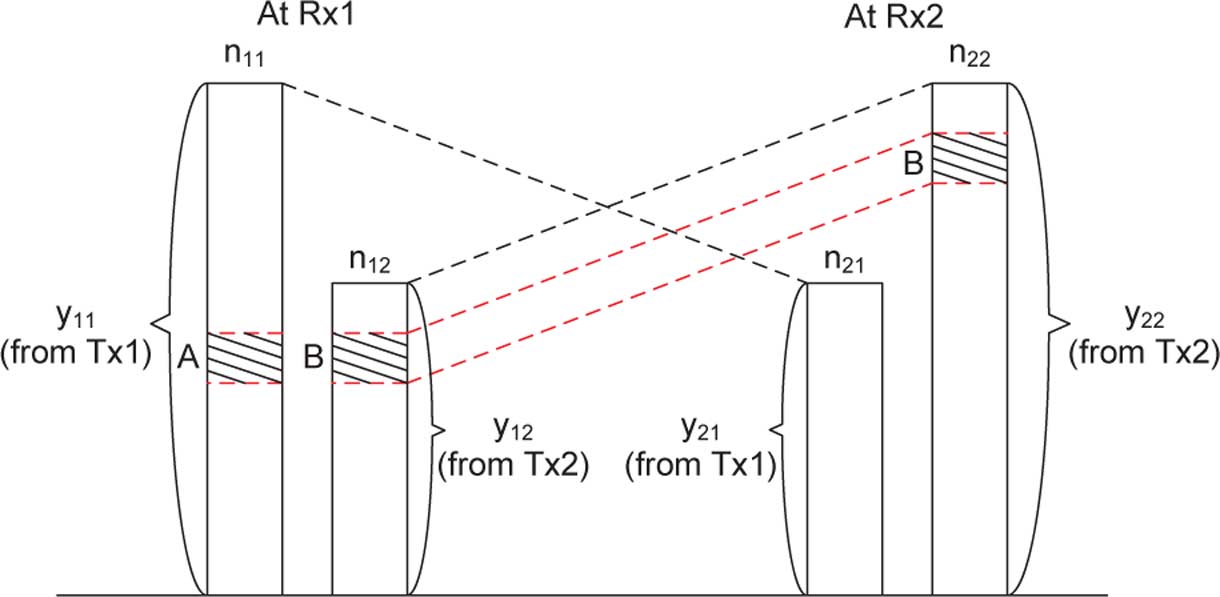
Now, we can formulate the sum-rate maximization problem as II. PROBLEM FORMULATION IN GAUSSIAN CHANNELS We consider the two-user Gaussian interference channel shown in The received signals of the two users are Note that involves both a combinatorial optimization of the decoding orders and a nonconvex optimization of the Throughout this paper, when we refer to the Han-Kobayashi scheme, we mean the Gaussian Han-Kobayashi scheme, unless stated otherwise.
. As a result, it is a hard problem from an IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Fig. 2. Our approach to solving problem optimization point of view which has not been addressed in the ference between the maximum achievable sum-rate using Gaussian successive decoding schemes and that using Gaussian Interestingly, we show that an "indirect" approach can ef- Han-Kobayashi schemes. This difference appears despite fectively and fruitfully provide approximately optimal solutions the fact that the sum-capacity of a Gaussian multiple access to the above problem Instead of directly working with the channel is achievable using successive decoding of Gaussian Gaussian model, we approximate the problem using the recently codewords. In the remainder of this section, we show an illus- developed deterministic channel model The approximate trative example that provides some intuition into this difference.
formulation successfully captures the key structure and intuition Suppose the th user uses two messages: a common of the original problem, for which we give a complete analyt- and a private message . We consider a power ical solution that achieves the constrained sum-capacity in all allocation to the encoded messages, and denote the power allo- channel parameters. Next, we translate this optimal solution in Denote the achiev- the deterministic formulation back to the Gaussian formulation, . In a Han-Kobayashi and show that the resulting solution is indeed close to the op- scheme, at each receiver, the common messages and the in- timum. This indirect approach of solving is outlined in tended private message are jointly decoded, treating the unin- Next, we provide an illustration of the following point: tended private message as noise. This gives rise to the achiev- Although the constraints for the achievable rate region with able rate region with any given power allocation as follows: Han-Kobayashi schemes share some similarities with thosefor the capacity region of multiple access channels, succes- sive decoding in interference channels does not always havethe same achievability as Han-Kobayashi schemes, (whereas time-sharing of successive decoding schemes does achieve thecapacity region of multiple access channels.) B. Successive Decoding of Gaussian Codewords versusGaussian Han-Kobayashi Schemes With Joint Decoding We first note that Gaussian superposition coding—succes- sive decoding is a special case of the Han-Kobayashi scheme, using the following observations. For the first user, if its message is decoded at the second receiver according to the decoding order , we categorize it into the common in- formation of the first user. Otherwise, is treated as noise at the second receiver, i.e., it appears after all the messages of the , and we categorize it into the private infor- mation of the first user. The same categorization is performed messages of the second user. Note that every mes- sage of the two users is either categorized as private informa-tion or common information. Thus, every successive decodingscheme is a special case of the Han-Kobayashi scheme, and hence the capacity region with successive decoding of Gaussiancodewords is included in that with Han-Kobayashi schemes.
However, the inclusion in the other direction is untrue, since Han-Kobayashi schemes allow joint decoding. In we will give a characterization of the dif- ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE whereas translate to In a successive decoding scheme, depending on the different decoding orders applied, the achievable rate regions have dif-ferent expressions. In the following, we provide and analyze theachievable rate region with the decoding orders at receiver 1 and2 being As a result, the maximum achievable sum-rates with the tively. The intuition obtained with these decoding orders holds Han-Kobayashi scheme and that with the successive decoding similarly for other decoding orders. 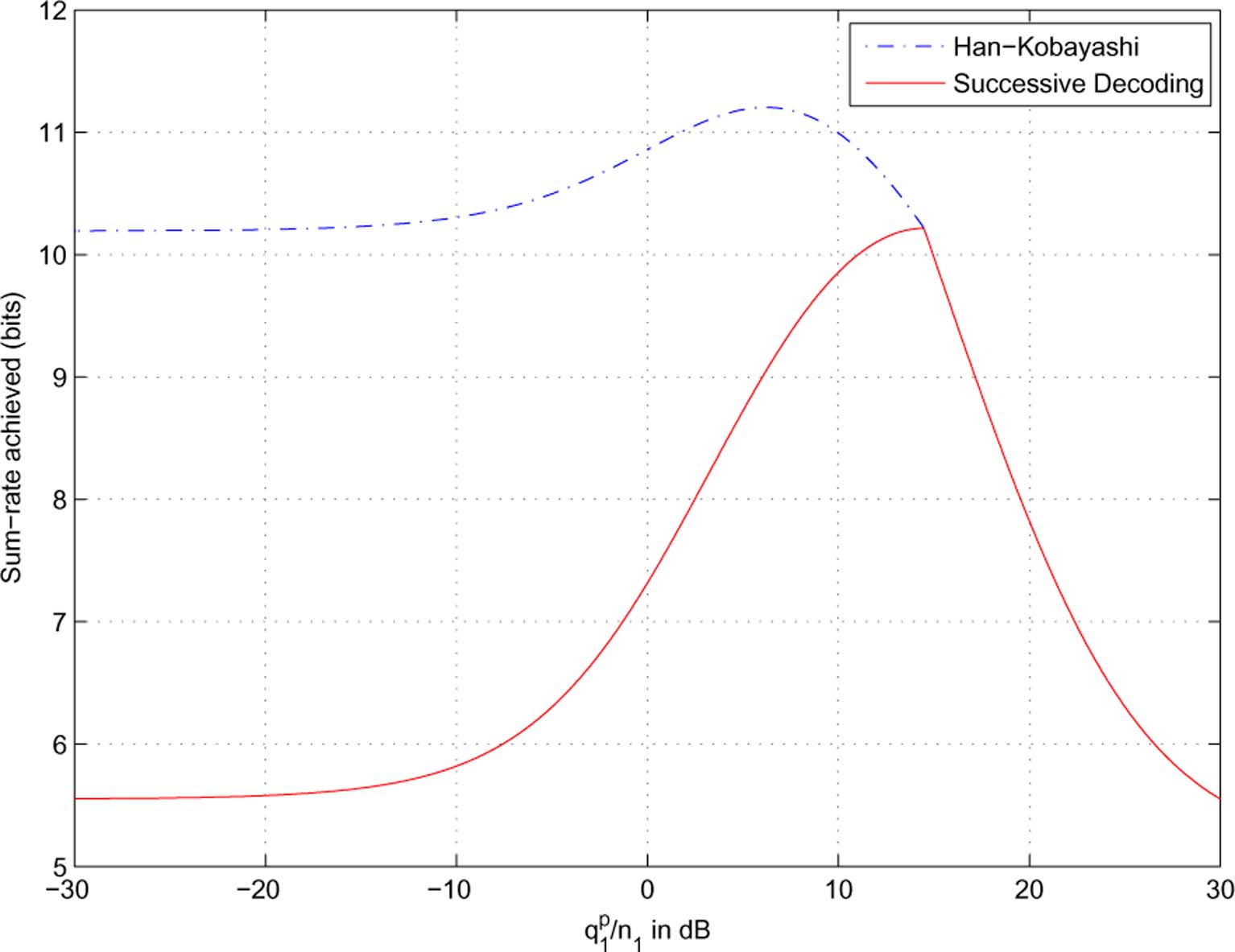With any given power allo- scheme are 10.19 and 5.56 bits, respectively. Here, the key intuition is as follows: for a common message, its individualrate constraints at the two receivers in a successive decodingscheme are tighter than those in a joint decodingscheme In we will see that lead to a nonsmooth behavior of the maximumachievable sum-rate using successive decoding of Gaussiancodewords. Finally, we connect the results shown in tothe results shown later in of Remark 2: In the optimal symmetric power allocation for a Han-Kobayashi scheme and that for a successive decodingscheme are and 14.5 dB, respectively, leading to sum-rates of 11.2 and 10.2 bits. This result corresponds to the performance evaluation at It is immediate to check that III. SUM-CAPACITY IN DETERMINISTIC INTERFERENCE To observe the difference between the maximum achievable A. Channel Model and Problem Formulation sum-rate with and that we examine thefollowing symmetric channel, In this section, we apply the deterministic channel model as an approximation of the Gaussian model on the two-user in- terference channel. We define in which we apply symmetric power allocation schemes with , and a power constraint of Remark 1: Note that . As indicated in of under this parameter setting, simply using successivedecoding of Gaussian codewords can have an arbitrarily large maximum achievable sum-rate loss compared to joint decodingschemes, as are the channel gains normalized by the We plot the sum-rates with the private message power noise power. Without loss of generality (WLOG), we assume sweeping from nearly zero to the maximum (30 . We note that the logarithms used in this paper dB) as in As observed, the difference between the two are taken to base 2. Now, counts the bit levels of the signal schemes is evident when the private message power sent from the th transmitter that are above the noise level at the sufficiently smaller than the common message power th receiver. Further, we define .) The intuition of why successive decoding of Gaussian codewords is not equivalent to the Han-Kobayashischemes is best reflected in the case of parameter setting, with which represent the cross channel gains relative to the directchannel gains, in terms of the number of bit-level shifts. Toformulate the optimization problem, we consider real numbers. (As will be shown later in Remark 5, with integerbit-level channel parameters, our derivations automatically giveinteger bit-level optimal solutions.)

IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Fig. 3. Illustrations of the difference between the achievable sum-rate with Han-Kobayashi schemes and that with successive decoding of Gaussian codewords.
Fig. 4. Two-user deterministic interference channel. Levels A and B interfere at the first receiver, and cannot be fully active simultaneously.
In the desired signal and the interference signal at both receivers are depicted.
are the sets of received infor- mation levels at receiver 1 that are above the noise level, fromusers 1 and 2, respectively.
are the sets of received information levels at receiver 2. A more concise representationis provided in • The sets of information levels of the desired signals at re- ceivers 1 and 2 are represented by the continuous intervals lines, where the leftmost points correspond to the most sig- Fig. 5. Interval representation of the two-user deterministic interference nificant (i.e., highest) information levels, and the points at correspond to the positions of the noise levels at both • The positions of the information levels of the interfering Note that an information level (or simply termed "level") is signals are indicated by the dashed lines crossing between a real point on a line, and the measure of a set of levels (e.g., the two parallel lines.
the length of an interval) equals the amount of information that ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE this set can carry. The design variables are whether or not each Problem does not include upper bounds on the number of level of a user's received desired signal carries information for . Such upper bounds can be added based on this user, characterized by the following definition.
Remark 3. We will analyze the cases without and with upperbounds on the number of messages. We first derive the con- Definition 1: is the indicator function on whether the strained sum-capacity in symmetric interference channels in the carry information for the th user.
remainder of this section. Results are then generalized using similar approaches to general (asymmetric) interference chan- information for the th B. Symmetric Interference Channels As a result, the rates of the two users are In this section, we consider the case where . WLOG, we normalize the amount of information levels by . Note that in symmetric channels, For an information level , we call it an active level for the th user, and otherwise an inactive level.
The constraints from superposition of Gaussian codewords with successive decoding translate to the followingComplementarity Conditions in the deterministic formulation.
are defined in The interpretation of and (26) are as follows: for any two levels each from one ofthe two users, if they interfere with each other at any of the tworeceivers, they cannot be simultaneously active. For example, ininformation levels from the first user and From Lemma 1, it is sufficient to only consider the case with second user interfere at the first receiver, and hence cannot be , and the case with fully active simultaneously. These complementarity conditions by symmetry as in Corollary 3 later.
have also been characterized using a conflict graph model in We next derive the constrained sum-capacity using succes- sive decoding for , first without upper bounds on the Remark 3: For any given function number of messages, then with upper bounds. We will see that joint segment within on it corresponds to a in symmetric channels, the constrained sum-capacity distinct message. Adjacent segments that can be so combined . Thus, we also use the maximum as a super-segment having on it, are viewed as one achievable symmetric rate, denoted by as a function of , segment, i.e., the combined super-segment. Thus, for two seg- as an equivalent performance measure.
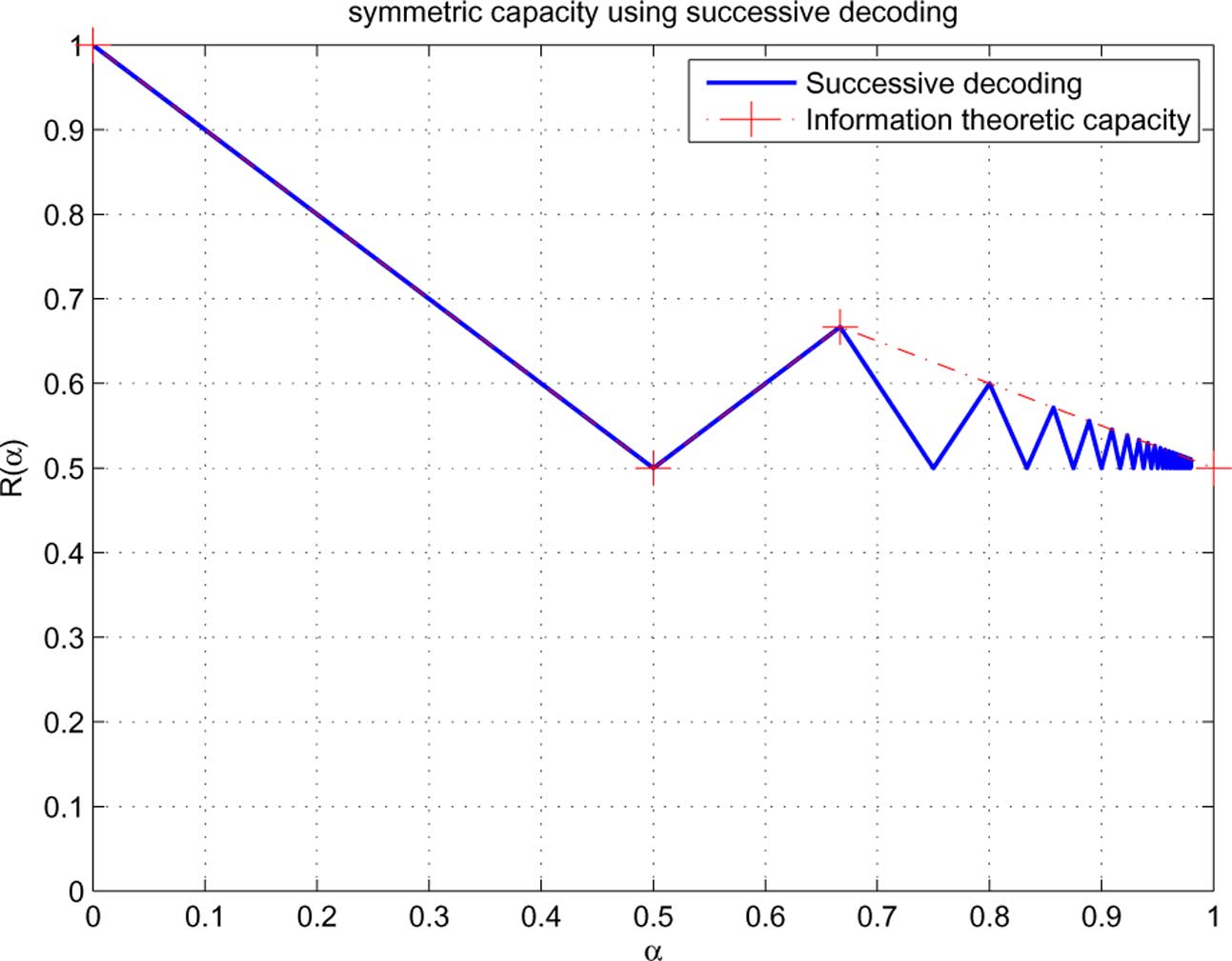
is thus one half of the optimal value of 1) Symmetric Capacity Without Constraint on the Number separated by the point have to correspond to two distinct of Messages: Theorem 1: In symmetric weak interference channels Finally, we note that , the constrained symmetric capacity, i.e., the maximum achievable symmetric rate using successive decoding [with and (29)], , is characterized by Thus, we have the following result: • In every interval Lemma 1: The parameter settings decreasing linear function.
• In every interval correspond to the same set of complementarity conditions.
increasing linear function.
We consider the problem of maximizing the sum-rate of the two users employing successive decoding, formulated as the following continuous support Remark 4: We plot in compared with the infor- (infinite dimensional) optimization problem: mation theoretic capacity The key idea in deriving the constrained sum-capacity is to decouple the effects of the complementarity conditions. Beforewe present the complete proof of Theorem 1, we first analyzethe following two examples that illustrate this decoupling idea.

IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Fig. 6. The symmetric capacity with successive decoding in symmetric deterministic weak interference channels.
Example 1, : As in we divide the with equal lengths.
From the complementarity conditions can be achieved by letting Example 2, : As in we divide lengths. For the same reasons as in the last example, Fig. 7. Two examples that illustrate the proof ideas of Theorem 1. (a) The ex- . (b) The example of  = can be achieved by letting Proof of Theorem 1: . We divide the interval ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE Fig. 8. Segmentation of the information levels, , where the first segments have length can be optimized independently of each other.
, and the last segment has length (cf. With these, the complementarity conditionsare equivalent to the following: . Hence can be solved by separately solving the following two subproblems: [Equations correspond to the shaded stripsin Similarly We now prove that the optimal value of is • (Achievability:) is achievable with We partition the set of all segments into two groups: • Equation are constraints on • Equation are constraints on Consequently, instead of viewing the (infinite number of)optimization variables as more convenient to view them as By symmetry, the solution of can be obtained sim-ilarly, and the optimal value is because there is no constraint between well. Therefore, the optimal value of is the complementarity conditions. In other words, IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Fig. 9. Segmentation of the information levels, As the above maximum achievable scheme is symmetric, • (Achievability:) is achievable with the symmetric capacity is is an increasing linear function of By symmetry, the solution of can be obtained simi- . Similarly to i), we divide the interval larly. Thus, the optimal value of is , where the first maximum achievable scheme is also characterized by segments have length , and the last segment has and the symmetric rate is complementarity conditions are equivalentto the following: is a decreasing linear function of . It can be verified iii) It is clear that , which is achievable with which is achievable by Similarly to i), with , can be solved by separately solving the following two subproblems: We summarize the optimal scheme that achieves the con- strained symmetric capacity as follows: Corollary 1: When , the constrained symmetric capacity is achievable with In the special cases when We now prove that the optimal value of is , the constrained symmetric capacity drops to

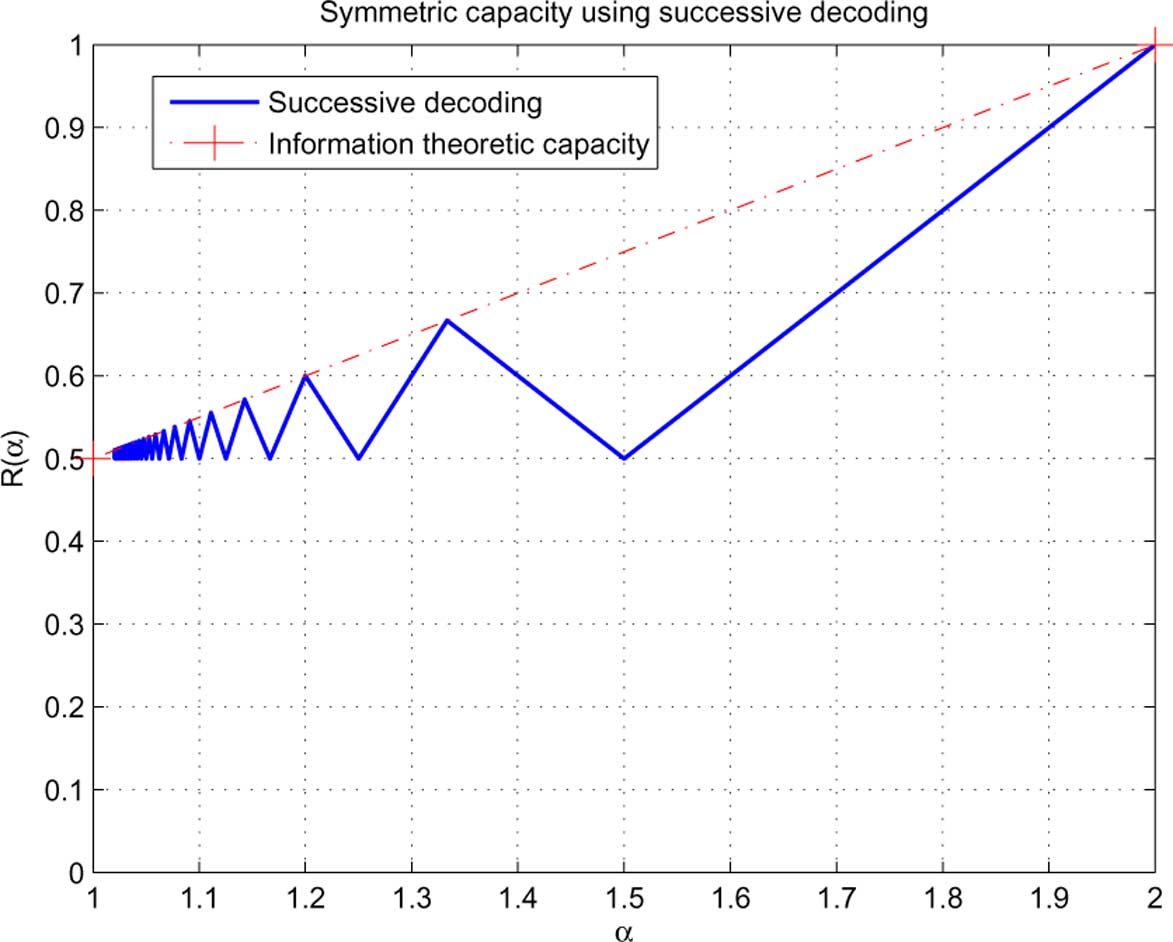
ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE Fig. 10. The symmetric capacity with successive decoding in symmetric deterministic strong interference channels.
also achievable by time sharing Clearly, the maximum achievable symmetric rate achieved willbe lower than . We start with the following two lemmas, whose proofs are relegated to We observe that the numbers of messages used by the two Lemma 2: If there exists a segment with an even index —in the above optimal schemes are as follows.
does not end at 1, such that Corollary 2: defined as in then Lemma 3: If there exists a segment with an odd index Remark 5: In the original formulation of the deterministic are considered to be integers, and the achievable scheme must also have integer bit-levels. In this case, is a rational number. As a result, the optimal scheme will consist of active segments that have rational bound- Recall that the optimal scheme requires that, for both aries with the same denominator . This indeed corresponds users, all segments in are fully inactive, and all segments to an integer bit-level solution.
are fully active. The above two lemmas show the cost From Theorem 1 (cf. it is interesting to see that the of violating if one of the segments in constrained symmetric capacity oscillates as a function of active for either user (cf. Lemma 2), or one of the segments in tween the information theoretic capacity and the baseline of .
becomes fully inactive for either user (cf. Lemma 3), the This phenomenon is a consequence of the complementarity con- resulting sum-rate cannot be greater than 1. We now establish ditions. In we further discuss the connections of this the following theorem.
result to other coding-decoding constraints.
Theorem 2: Denote by the number of messages Finally, from Lemma 1, we have the following corollary on used by the th user. When the maximum achievable symmetric rate with successive de- , the maximum achievable sum-rate is 1.
coding in strong interference channels.
Proof: WLOG, assume that there is a constraint of Corollary 3: In symmetric strong interference channels i) First, the sum-rate of 1 is always achievable with in compared with the information theoretic capacity ii) If there exists , such that either 2) The Case With a Limited Number of Messages: In this , then from Lemma 2, subsection, we find the maximum achievable sum/symmetric the achieved sum-rate is no greater than 1.
rate using successive decoding when there are constraints on the in the interior of maximum number of messages for the two users, respectively.

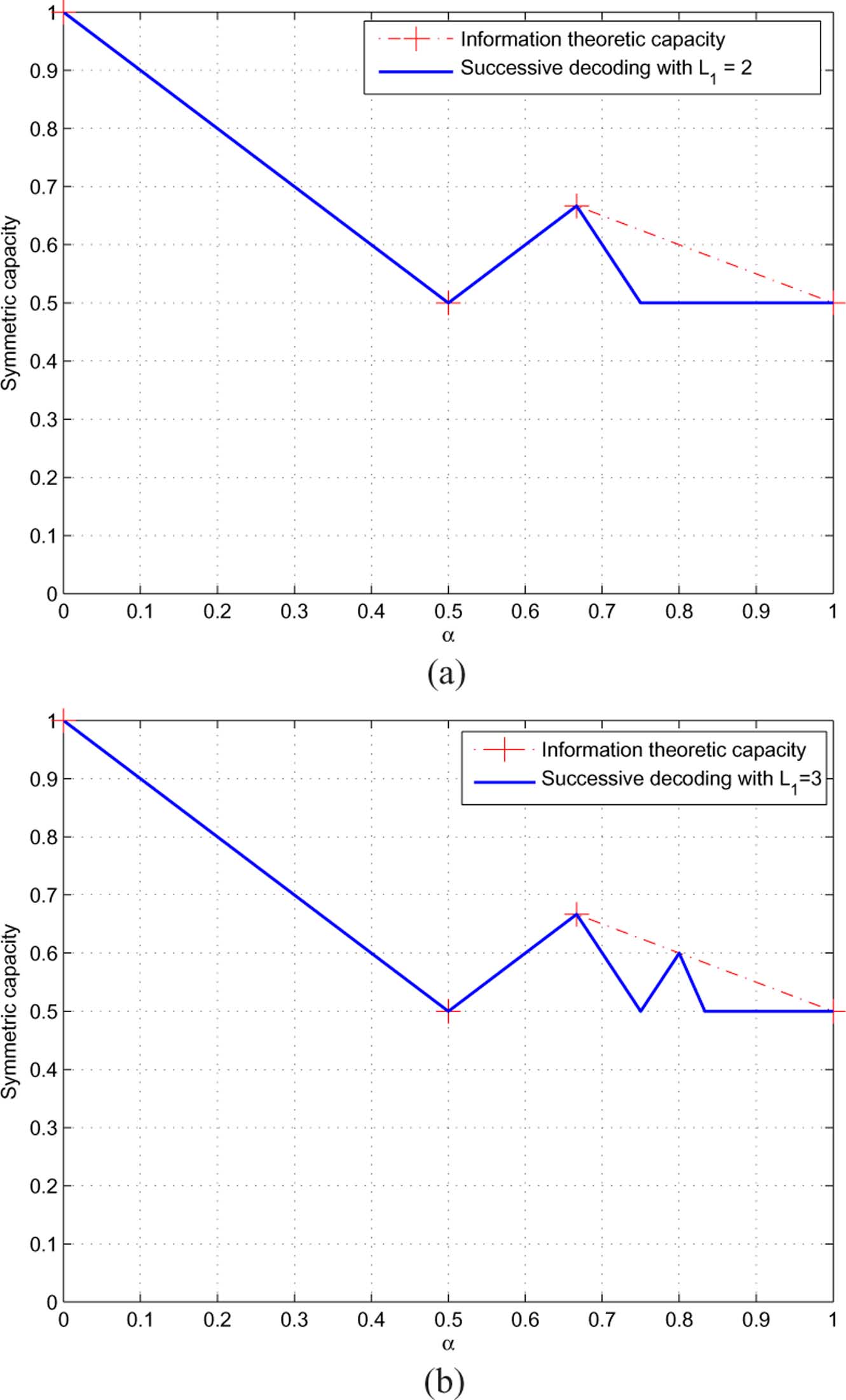
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Fig. 11. The maximum achievable symmetric rate with a limited number of messages. (a) Maximum achievable symmetric rate with L  2. (b) Maximumachievable symmetric rate with L  3.
separates the two segments Comparing Theorem 2 to Corollary 2, we conclude that if the first user. From Remark 3, have to be two dis- number of messages used for either of the two users is fewer tinct messages provided that both of them are (at least partly) than the number used in the optimal scheme (as in Corollary active for the first user. On the other hand, there are 2), the maximum achievable symmetric rate drops to is illustrated in with the number of messages of the first user is upper bounded by Complete solutions (without and with constraints on the . In other words, there must be a segment in number of messages) in asymmetric channels follow similar is fully inactive for the first user. By Lemma 3, in this case, the ideas, albeit more tediously. Detailed discussions are relegated achieved sum-rate is no greater than 1.
ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE IV. APPROXIMATE MAXIMUM ACHIEVABLE SUM-RATE WITH SUCCESSIVE DECODING IN GAUSSIAN INTERFERENCE CHANNELS In this section, we turn our focus back to the two-user Gaussian interference channel, and consider the sum-ratemaximization problem Based on the relation between thedeterministic channel model and the Gaussian channel model,we translate the optimal solution of the deterministic channelinto the Gaussian channel. We then derive upper bounds onthe optimal value of and evaluate the achievability of ourtranslation against these upper bounds.
A. Achievable Sum-Rate Motivated by the Optimal Schemein the Deterministic Channel As the deterministic channel model can be viewed as an ap- proximation to the Gaussian channel model, optimal schemesof the former suggest approximately optimal schemes of thelatter. In this subsection, we show the translation of the op-timal scheme of the deterministic channel to that of the Gaussianchannel. We show in detail two forms (simple and fine) of thetranslation for symmetric interference channels The translation for asymmetric channels can be derived simi- Fig. 12. The optimal schemes in the symmetric deterministic interferencechannel. (a) Weak interference channel. (b) Strong interference channel.
larly, albeit more tediously.
1) A Simple Translation of Power Allocation for the Mes- sages: Recall the optimal scheme for symmetric deterministicinterference channels (Corollary 1,) as plotted in represent the segments (or messages as translated deterministic scheme, the key property that ensures optimality to the Gaussian channel) that are active for the th user. Recall is the following: Corollary 4: A message that is decoded at both re- ceivers is subject to the same achievable rate constraint at both For example, in the optimal deterministic schemes (cf.
to the right (i.e., lower information levels) is subject to an achievable rate con- in the deterministic channel approximately corresponds to a at the first receiver, and that of power scaling factor of in the Gaussian channel. Accord- second receiver, with . In weak interference ingly, a simple translation of the symmetric optimal schemes (cf. into the Gaussian channel is given as follows.
messages that are decoded at both receivers, whereas are decoded only at their intended receiver (and treated Algorithm 1: A simple translation by direct power scaling as noise at the other receiver.) In strong interference channels,all messages are decoded at both receivers.
Step 1: Determine the number of messages According to Corollary 4, we show that a finer translation each user as the same number used in the optimal deterministic of the power allocation for the messages is achieved by equal- channel scheme.
izing the two rate constraints for every common message. (How- ever, rates of different common messages are not necessarily thesame.) In what follows, we present this translation for weak in- , and normalize the terference channel and strong interference channel, respectively.
Weak Interference Channel, : As the first step of determining the power allocations, we give the followinglemma on the power allocation of message , and normalize the 2) A Finer Translation of Power Allocation for the Messages: In this part, for notational simplicity, we assume WLOG that noise at the second (first) receiver, with IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 case, there is only one message for each user (as its private Numerical evaluations of the above simple and finer trans- message.) Rate constraint equalization is not needed.
lations of the optimal schemes for the deterministic channel into that for the Gaussian channel are provided later in at both receivers. To equalize their rate constraints at both receivers, we must have the power allocation as follows: B. Upper Bounds on the Maximum Achievable Sum-Rate With Successive Decoding of Gaussian Codewords Next, we observe that after decoding In this subsection, we provide two upper bounds on the optimal solution of for general (asymmetric) weak inter- ceivers, determining can be transformed to ference channels. More specifically, the bounds are derived an equivalent first step problem with for the maximum achievable sum-rate with Han-Kobayashi of the transformed problem gives the correct equal- schemes, which automatically upper bound that with successive izing solution for of the original problem. In general, we decoding of Gaussian codewords (as shown in have the following recursive algorithm in determining We will observe that, for weak interference channels, the two bounds have complementary efficiencies, i.e., each being tightin a different regime of parameters. For strong interference Algorithm 2.1, A finer translation by adapting channels, the information theoretic capacity is known using rate constraint equalization; weak interference channel which is achievable by jointly decoding of all the messagesfrom both users.
Similarly to we denote by and terminate.
sage of the th user, and the common message to be the power allocated to each private mes- , 2. Then, the power of the common message . Go to Step 1.
. WLOG, we normalize the channel parame- . Denote the rates of Strong Interference Channel, : As the first . The maximum achievable sum-rate of Gaussian step of determining the power allocations, we give the following Han-Kobayashi schemes is thus the following: lemma on the power allocation of (with the proof found are always decoded at both re- ceivers. Moreover, , and the power allocation of To bound we select two mutually exclusive subsets of . In this case, there is only one . Then, with each subset of the message for each user. Rate constraint equalization is not constraints, a relaxed sum-rate maximization problem can be solved, leading to an upper bound on the original maximum . To equalize the rate constraints achievable sum-rate ) at both receivers, we must have the The first upper bound on the maximum achievable sum-rate power allocation as follows: is as follows [whose proof is immediate from Lemma 6: The maximum achievable sum-rate using Han- Kobayashi schemes is upper bounded by Next, we observe that after decoding ceivers, determining can be transformed to an equivalent first step problem with of the transformed problem gives the correct equal- izing solution for of the original problem. In general, we have the following recursive algorithm in determining Algorithm 2.2, A finer translation by adapting using rate constraint equalization; strong interference channel Computation of the Upper Bound Note that and terminate.
. Go to Step 1.
ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE Lemma 7: The maximum achievable sum-rate using Han- Kobayashi schemes is upper bounded by the minimum of is Computation of the Upper Bound Note that Now, consider the halfspace linear constraint where is a function only of , and is a function only of can each be solved by taking the first order derivatives, and checking the stationary points and the boundary points.
We combine the two upper bounds and as the fol- lowing theorem.
Theorem 3: The maximum achievable sum-rate using . Thus, depending on the sign Gaussian superposition coding-successive decoding is upper , we have the following two cases.
. Then, gives an upper bound C. Performance Evaluation . Consequently, to maximize the optimal solution is . Thus, maximizing is equivalent to We numerically evaluate our results in symmetric Gaussian interference channels. The is set to be 30 dB. We first eval- uate the performance of successive decoding in weak interfer- ence channels and then in strong interference channels.
1) Weak Interference Channel: We sweep the parameter in which the objective is monotonic, and the solution is approximate optimal transmission scheme is simply treatinginterference as noise without successive decoding.
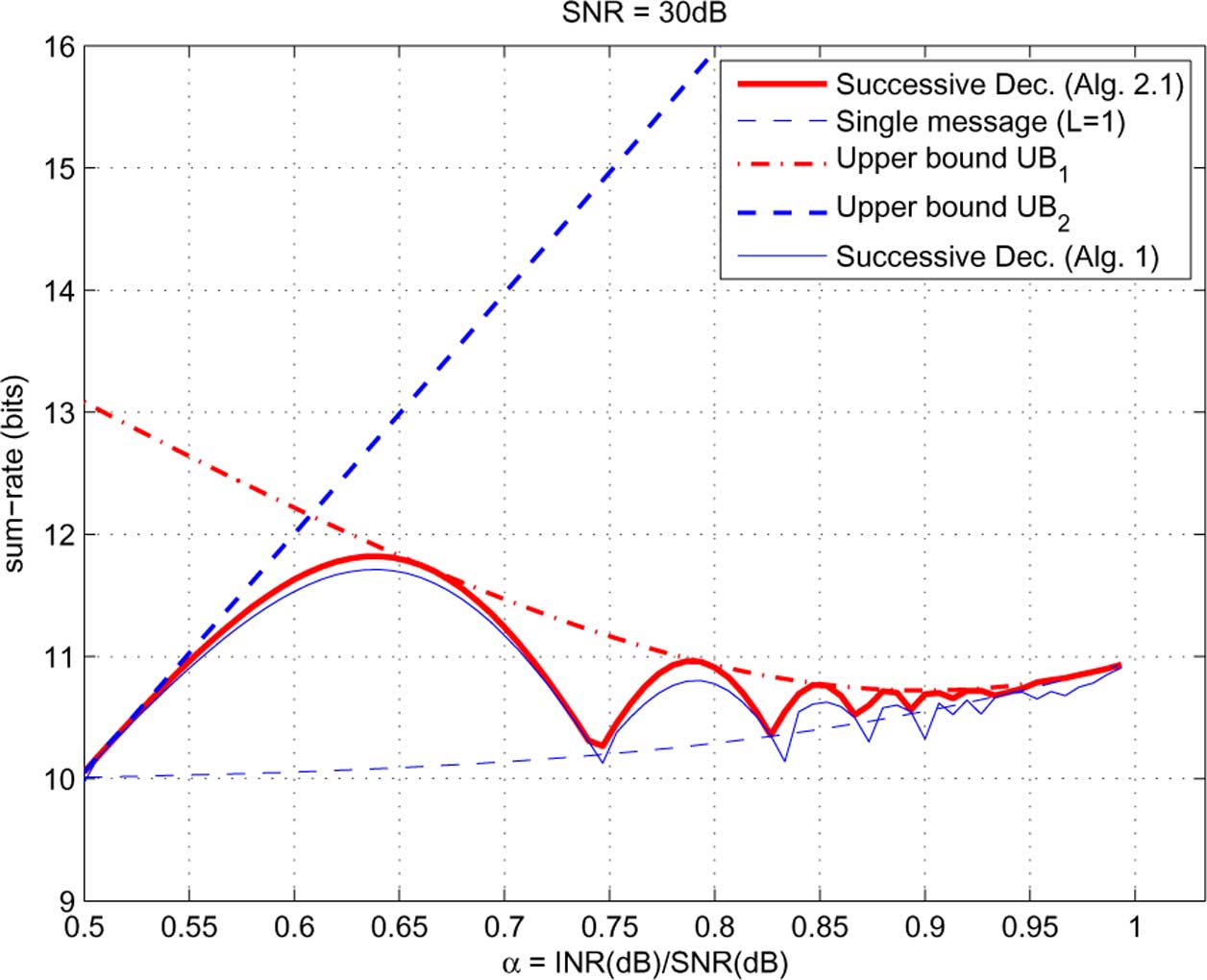
. Then, gives a lower bound on In the simple translation by Algorithm 1 and the finer translation by Algorithm 2.1 are evaluated, and the two upperbounds derived above are computed. The maximum achievable sum-rate with a single message for each user is also computed, and is used as a baseline scheme for Consequently, to maximize the optimal solution is , which is a linear We make the following observations: . Substituting this into we need to solve the • The finer translation of the optimal deterministic scheme following problem: by Algorithm 2.1 is strictly better than the simple trans-lation by Algorithm 1, and is also strictly better than theoptimal single message scheme.
• The first upper bound is tighter for higher in this example), while the second upper bound are constants determined by is tighter for lower in this example).
. Now, can be solved by taking the first • A phenomenon similar to that in the deterministic chan- derivative w.r.t.
, and checking the two stationary points and nels appears: the maximum achievable sum-rate with the two boundary points.
successive decoding of Gaussian codewords oscillates In the other halfspace , the same procedure as above can between that with Han-Kobayashi schemes and that with be applied, and the maximizer of within can be found.
single message schemes.
Comparing the two maximizers within • The largest difference between the maximum achievable we get the global maximizer of sum-rate of successive decoding and that of single mes- The second upper bound on the maximum achievable sum- sage schemes appears at around rate is as follows [whose proof is immediate from about 1.8 bits.

IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Fig. 13. Performance evaluation in symmetric weak interference channel: achievability versus upper bounds.
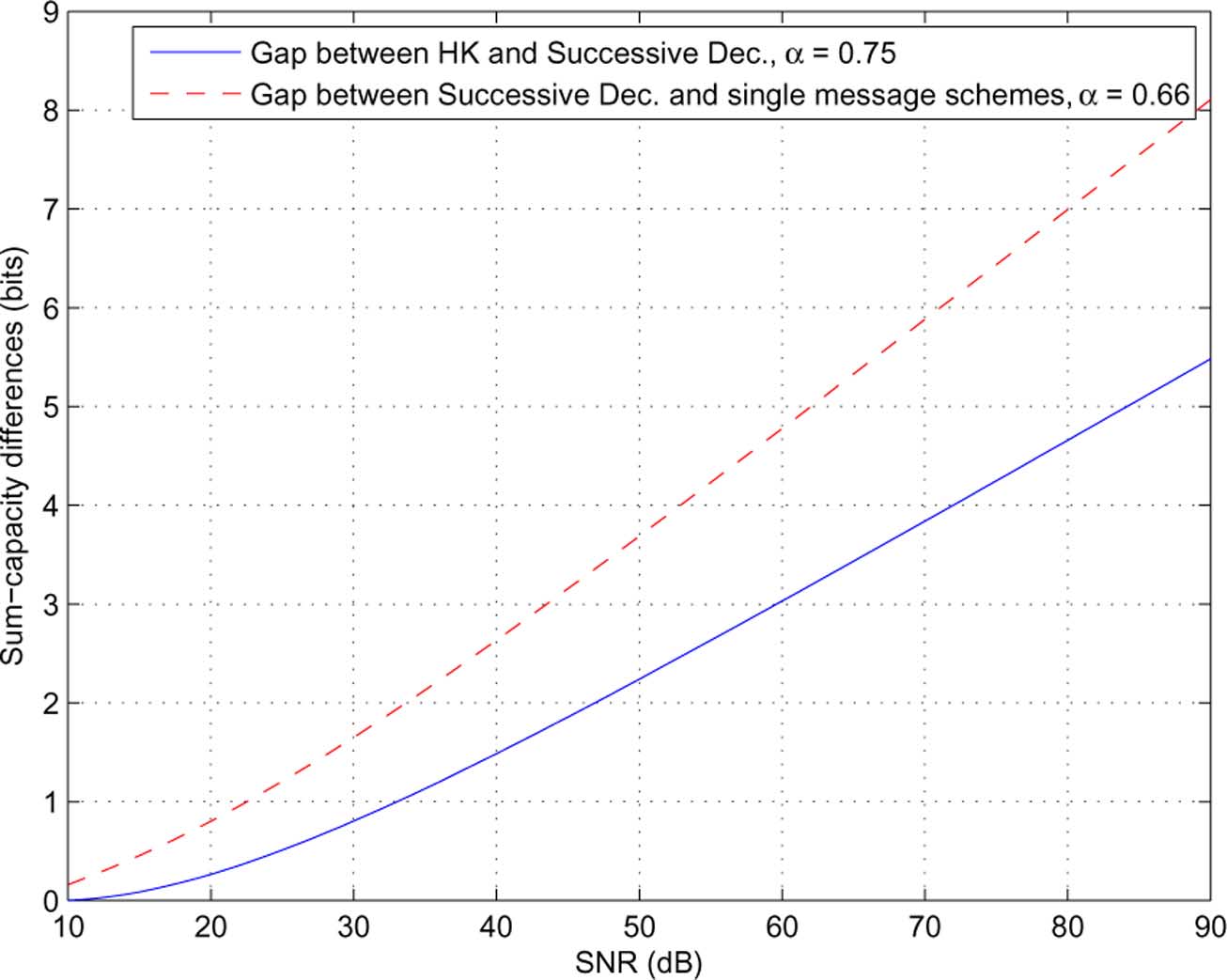
Fig. 14. Maximum achievable sum-rate differences: Han-Kobayashi versus successive decoding at  = 0:75, and successive decoding versus the optimal singlemessage scheme at  = 0:66.
• The largest difference between the maximum achievable shown with the deterministic channel model (cf. indicate sum-rate of successive decoding and that of joint decoding that these differences can go to infinity as (Han-Kobayashi schemes) appears at around because a rate point on the symmetric capacity curve . This corresponds to the same parameter setting as in the deterministic channel has the following interpretation discussed in (cf. We see that with of generalized degrees of freedom in the Gaussian channel , this largest maximum achievable sum-rate dif- ference is about 1.0 bits.
For this particular case with maximum achievable sum-rate differences (1.8 bits and 1.0 bits) may not seem very large. However, the capacity curves

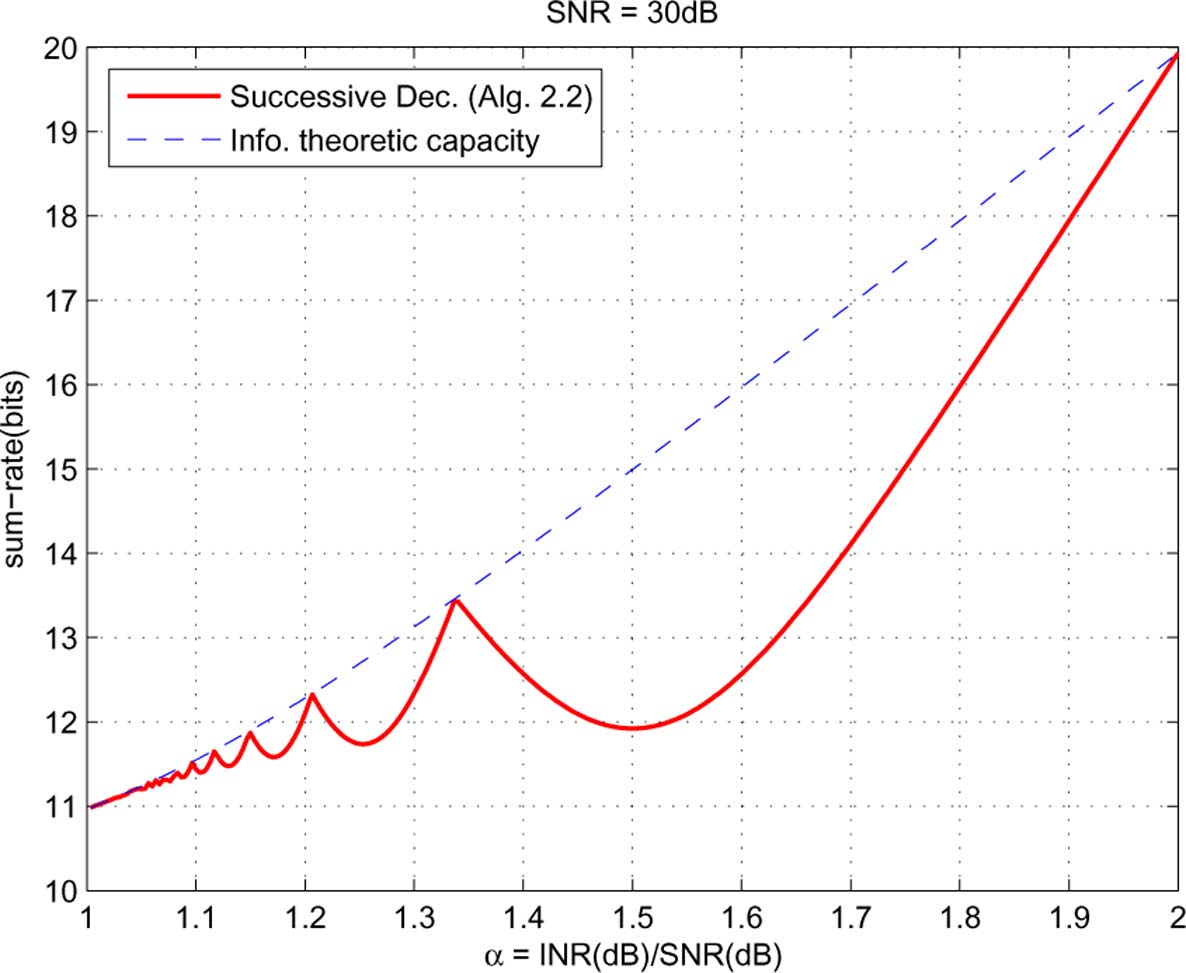
ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE Fig. 15. Performance evaluation in symmetric strong interference channel: successive decoding versus information theoretic capacity.
In the finer translation by Algorithm 2.2 is evaluated is the symmetric capacity in the two-user symmetric Gaussian and compared with the information theoretic sum-capacity channel as a function of Interestingly, an oscillation phenomenon similar to that in the deterministic channel case (cf. is observed.
finite gap of the achievable rates in the deterministic channelindicates a rate gap that goes to infinity as V. CONCLUDING REMARKS AND DISCUSSION Gaussian channel. To illustrate this, we plot the following max- In this paper, we studied the problem of sum-rate maxi- imum achievable sum-rate differences in the Gaussian channel, mization with Gaussian superposition coding and successive growing from 10 to 90 dB: decoding in two-user interference channels. This is a hard • The maximum achievable sum-rate gap between Gaussian problem that involves both a combinatorial optimization of superposition coding-successive decoding schemes and decoding orders and a nonconvex optimization of power allo- single message schemes, with cation. To approach this problem, we used the deterministic channel model as an educated approximation of the Gaussian channel model, and introduced the complementarity condi- tions that capture the use of successive decoding of Gaussian codewords. We solved the constrained sum-capacity of the As observed, the maximum achievable sum-rate gaps in- deterministic interference channel under the complementarity crease asymptotically linearly with conditions, and obtained the constrained capacity achieving schemes with the minimum number of messages. We showed 2) Strong Interference Channel: We sweep the parameter that the constrained sum-capacity oscillates as a function of . As the information theoretic the cross link gain parameters between the information the- sum-capacity in strong interference channel can be achieved by oretic sum-capacity and the sum-capacity with interference having each receiver jointly decode all the messages from both treated as noise. Furthermore, we showed that if the number users we directly compare the achievable sum-rate using of messages used by either of the two users is fewer than its successive decoding with this joint decoding sum-capacity (in- minimum capacity achieving number, the maximum achievable stead of upper bounds on it). This joint decoding sum-capacity sum-rate drops to that with interference treated as noise. Next, can be computed as follows: we translated the optimal schemes in the deterministic channelto the Gaussian channel using a rate constraint equalization technique, and provided two upper bounds on the maximumachievable sum-rate with Gaussian superposition coding andsuccessive decoding. Numerical evaluations of the translationand the upper bounds showed that the maximum achievablesum-rate with successive decoding of Gaussian codewordsoscillates between that with Han-Kobayashi schemes and thatwith single message schemes.
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 Next, we discuss some intuitions and generalizations of the successive decoding and that using joint decoding can be significant for typical s in practice.
Recently, the role of feedback in further increasing the in- A. Complementarity Conditions and Gaussian Codewords formation theoretic capacity region has been studied In these work, the deterministic channel model was also em- The complementarity conditions in the deter- ployed as an approximation of the Gaussian channel model, ministic channel model has played a central role that leads to the leading to useful insights in the design of near-optimal trans- discovered oscillating constrained sum-capacity (cf. Theorem mission schemes with feedback. We note that, in deterministic 1). The intuition behind the complementarity conditions is as channels, allowing feedback implicitly assumes that modulo-2 follows: At any receiver, if two active levels from different users sums can be decoded. In Gaussian channels, it remains an inter- interfere with each other, then no information can be recovered esting open question to find the maximum achievable sum-rate at this level. In other words, the sum of interfering codewords using successive decoding of Lattice codewords with feedback.
provides nothing helpful.
This is exactly the case when random Gaussian codewords C. Symbol Extensions and Asymmetric Complex Signaling are used in Gaussian channels with successive decoding,because the sum of two codewords from random Gaussian We have focused on two-user complex Gaussian interference codebooks cannot be decoded as a valid codeword. This is the channels with constant channel coefficients, and have assumed reason why the usage of Gaussian codewords with successive that symbol extensions are not used, and circularly symmetric decoding is translated to complementarity conditions in the complex Gaussian distribution is employed in codebook gen- deterministic channels. (Note that the preceding discussions eration. With symbol extensions and asymmetric complex sig- do not apply to joint decoding of Gaussian codewords as in naling the maximum achievable sum-rate using successive Han-Kobayashi schemes.) decoding can be potentially higher. It has been shown that, inthree or more user interference channels, higher sum-degrees of B. Modulo-2 Additions, Lattice Codes and Feedback freedom can be achieved by interference alignment if symbolextensions and asymmetric complex signaling are used In the deterministic channel, a relaxation on the comple- In two-user interference channels, however, interference align- mentarity conditions is that the sum of two interfering active ment is not applicable, and it remains an interesting open ques- levels can be decoded as their modulo-2 sum. As a result, the tion to find the maximum achievable sum-rate with successive aggregate of two interfering codewords still provides something decoding considering symbol extensions and asymmetric com- valuable that can be exploited to achieve higher capacity. This plex signaling.
assumption is part of the original formulation of the determin-istic channel model with which the information theoretic capacity of the two-user interference channel (cf. for PROOFS OF LEMMA 2 AND 3 the symmetric case) can be achieved with Han-Kobayashischemes Proof of Lemma 2: By symmetry, it is sufficient to prove In Gaussian channels, to achieve an effect similar to de- that does not end coding the modulo-2 sum with successive decoding, Lattice codes are natural candidates of the coding schemes. This is Now, consider the sum-rate achieved within because Lattice codebooks have the group property such that can be partitioned into three the sum of two lattice codewords can still be decoded as a valid codeword. Such intermediate information can be decoded first and exploited later during a successive decoding procedure, in order to increase the achievable rate. For this to succeed in degenerate.) Note that interference channels, alignment of the signal scales becomes • From the achievable schemes in the proof of Theorem 1, essential However, our preliminary results have shown the maximum achievable sum-rate within that the ability to decode the sum of the Lattice codewords does not increase the maximum achievable sum-rate for low and s. In the above setting of is typically considered as a high in practice) numerical • By the assumed condition, computations show that the maximum achievable sum-rate using successive decoding of lattice codewords with alignment Therefore, under the assumed condition, the maximum achiev- of signal scales is lower than the previously shown achievable able sum-rate within is achievable with sum-rate using successive decoding of Gaussian codewords (cf.
for the entire range of Furthermore, from the proof of Theorem 1, we know that reason is that the cost of alignment of the signal scales turns out the maximum achievable sum-rate within is achievable with to be higher than the benefit from it, if is not sufficiently high. In summary, no matter using Gaussian codewords or the maximum achievable schemes within Lattice codewords, the gap between the achievable rate using ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE Fig. 16. C partitioned into three parts for Lemma 2.
Fig. 17. C partitioned into three parts for Lemma 3.
a sum-rate of 1 is achieved, and this is the maximum achievable Furthermore, from the proof of Theorem 1, we know that sum-rate given the assumed condition.
the maximum achievable sum-rate within is achievable with Proof of Lemma 3: By symmetry, it is sufficient to prove the maximum achievable schemes within Now, consider the sum-rate achieved within a sum-rate 1 is achieved, and this is the maximum achievable can be partitioned into three parts: sum-rate given the assumed condition.
can be degenerate.) Note that: • From the achievable schemes in the proof of Theorem 1, SUM-CAPACITY OF DETERMINISTIC ASYMMETRIC the maximum achievable sum-rate within INTERFERENCE CHANNELS In this section, we consider the general two-user interference • By the assumed condition, channel where the parameters Therefore, under the assumed condition, the maximum achiev- trary. Still, WLOG, we make the assumptions that able sum-rate within is achievable with . We will see that our approaches in the symmetric channel can be similarly extended to solving the constrained IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 sum-capacity in asymmetric channels, without and with con- straints on the number of messages.
From Lemma 1, it is sufficient to consider the following three By the same argument as in the proof of Theorem 1, the op- timal solution of is given by A. Sum-Capacity Without Constraint on the Number of Also, the optimal solution of is given by We provide the optimal scheme that achieves the constrained sum-capacity in each of the three cases in respectively.
: This is by definition equivalent Consequently, we have the following theorem.
As depicted in interval is partitioned into Theorem 4: A constrained sum-capacity achieving scheme ; the last segment ending at 1 has the length of the proper residual. Intervalis partitioned into segments ; the last segment ending at 1 has the length of the proper residual.
Similarly to as in the previous analysis for the symmetric and the maximum achievable sum-rate is readily computable channels, we partition the optimization variables As depicted in interval is partitioned into ; the last segment ending at 1 has the length of the proper residual. Interval is partitioned into As there is no constraint between ment ending at 1 has the length of the proper residual. (The in- plementarity conditions similarly to and dexing is not consecutive as we consider the sum-rate maximization is decoupled into two separate as degenerating to empty sets.) does not conflict with any levels of . On all the other segments, the sum-rate maximization problem is ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE  n , n < n , n  n , and n  n , scheme I (nonoptimal).
By the same argument as in the proof of Theorem 1, the optimal does not conflict with any levels of solution of is given by . On all the other segments, the sum-rate maximization problem is again and the optimal solution is given by Thus, a sum-capacity achieving scheme is simply Thus, a sum-capacity achieving scheme is This is by definition equivalent to . Note that by Lemma 1, it is sufficient to only consider the , (because in case is partitioned into segments . As depicted in interval partitioned into segments ; the last segment ending at 1 has the length of the ; the last segment ending at 1 has the length of the proper proper residual. Interval is partitioned into residual. Interval is partitioned into segments ; the last segment ending at 1 has the the last segment ending at 1 has the length of the proper residual.
length of the proper residual.
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012  n , n < n , n  n , and n  n , scheme II (optimal).
Compare with Case 1 of and note the simi- Noting the similarities between and we see that larities between and we apply the same partition of the optimal solution of the two cases are the same: the optimization variables and the sum-rate maximization is decoupled in the same way into two separate problems : This is by equivalent to and However, while the optimal solution of is still . Note that by Lemma 1, it is sufficient to only given by the optimal solution of is no longer given by consider the case where , (because in case , the optimal solution of is given by is partitioned into seg- ; the last segment ending at 1 has the Thus, a sum-capacity achieving scheme is given by length of the proper residual. Interval , depicted as in tioned into segments : Comparing with Case 2 of the last segment ending at 1 has the length of the proper (cf. with the same definition of and the same partition of , the segmentation is does not conflict with any levels of . On all the other segments, the ZHAO et al.: MAXIMUM ACHIEVABLE SUM-RATE sum-rate maximization problem is again As for the second user. On the other hand, there are optimal solution is given by , whereas the number of messages is . In other words, for the second user, there must be a segment with an odd index that is fully in- Thus, a sum-capacity achieving scheme is active. By Lemma 9, in this case, Similarly to the symmetric case, we conclude that if the number of messages used for either user is fewer than the Summarizing the discussions of the six parameter settings (cf.
number used in the optimal scheme the maximum achiev- and in this subsection, we observe: able sum-rate drops to 1.
Remark 6: Except for Case 1 of the op- timal schemes for the other cases all have the property that only one message is used for each user.
PROOF OF LEMMA 4 AND 5 The Case With a Limited Number of Messages: In this sub- Proofs of Lemma 4: At the first receiver, the mes- section, we extend the sum-capacity results in is decoded by treating all other messages to the asymmetric channels when there are upper bounds onthe number of messages for the two users, respec- as noise, and has an tively. From Remark 6, we only need to discuss Case 1 of (cf. with its corresponding notations.
At the second receiver, is first decoded and peeled off.
Similarly to the symmetric channels, we generalize Lemma 2 is also decoded at the second receiver (by treating and 3 to the following two lemmas for the general (asymmetric) as noise) it has an channels, whose proofs are exact parallels to those of Lemma 2 . To equalize the rate constraints for at both receivers, we need does not end at 1, such that does not end at 1, such that . It implies that we should not decode at the second receiver, i.e., is the only message of the th user, which is treated as noise at the other receiver.
Proof of Lemma 5: At the second receiver, the We then have the following generalization of Theorem 2 to is decoded by treating all other messages the general (asymmetric) channels.
as noise, and has an Theorem 5: Denote by the number of messages used by the th user in any scheme, and denote by the dictated number At the first receiver, is first decoded and peeled off. Next, of messages used by the th user in the constrained sum-capacity is decoded by treating achieving scheme Then, if noise, and has an the rate constraints for at both receivers, we need Proof: Consider can be proved similarly.) i) The sum-rate of 1 is always achievable with . It implies that, ii) If there exists does not end at 1, even if the common message is allocated with all the , then from Lemma 8, power , it still has a higher rate constraint at the second (first) receiver than at the first (second) receiver.
iii) If for every does not end at 1, there in the interior of does not end at 1, separates the two segments [1] Y. Zhao, C. W. Tan, A. S. Avestimehr, S. N. Diggavi, and G. J. Pottie, "On the sum-capacity with successive decoding in interference chan- user. From Remark 3, have to be two distinct nels," in Proc. IEEE Int. Symp. Inf. Theory, St. Petersburg, Russia, Jul.
messages provided that both of them are (at least partly) active 2011, pp. 1494–1498.
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 6, JUNE 2012 [2] R. H. Etkin, D. Tse, and H. Wang, "Gaussian interference channel ca- Chee Wei Tan (M'08) received the M.A. and Ph.D. degrees in electrical
pacity to within one bit," IEEE Trans. Inf. Theory, vol. 54, no. 12, pp.
engineering from Princeton University, Princeton, NJ, in 2006 and 2008, 5534–5562, 2008.
[3] M. Ebrahimi, M. Maddah-Ali, and A. Khandani, "Power allocation and Previously, he was a Postdoctoral Scholar at the California Institute of Tech- asymptotic achievable sum-rates in single-hop wireless networks," in nology (Caltech), Pasadena. He is currently an Assistant Professor at City Uni- Proc. Conf. Inf. Sci. Syst., Mar. 2006, pp. 498–503.
versity Hong Kong. He was a Visiting Faculty at Qualcomm R&D, San Diego, [4] V. Annapureddy and V. Veeravalli, "Gaussian interference networks: CA, in 2011. His research interests are in wireless and broadband communica- Sum capacity in the low-interference regime and new outer bounds tions, signal processing and nonlinear optimization.
on the capacity region," IEEE Trans. Inf. Theory, vol. 55, no. 7, pp.
Dr. Tan was the recipient of the 2008 Princeton University Wu Prize for Ex- 3032–3050, 2009.
cellence and 2011 IEEE Communications Society AP Outstanding Young Re-searcher Award. He currently serves as an Editor for the IEEE T [5] A. Motahari and A. Khandani, "Capacity bounds for the Gaussian inter- ON COMMUNICATIONS.
ference channel," IEEE Trans. Inf. Theory, vol. 55, no. 2, pp. 620–643,Feb. 2009.
[6] X. Shang, G. Kramer, and B. Chen, "A new outer bound and the noisy-interference sum-rate capacity for Gaussian interference chan- A. Salman Avestimehr (S'04–M'09) received the B.S. degree in electrical en-
nels," IEEE Trans. Inf. Theory, vol. 55, no. 2, pp. 689–699, Feb. 2009.
gineering from Sharif University of Technology, Tehran, Iran, in 2003 and the [7] Z. Luo and S. Zhang, "Dynamic spectrum management: Complexity M.S. degree and Ph.D. degree in electrical engineering and computer science, and duality," IEEE J. Sel. Topics Signal Process., vol. 2, no. 1, pp.
both from the University of California, Berkeley, in 2005 and 2008, respectively.
57–73, 2008.
He is currently an Assistant Professor at the School of Electrical and Com- [8] C. W. Tan, S. Friedland, and S. H. Low, "Spectrum management in puter Engineering, Cornell University, Ithaca, NY. He was also a Postdoctoral multiuser cognitive wireless networks: Optimality and algorithm," Scholar at the Center for the Mathematics of Information (CMI), California In- IEEE J. Sel. Areas Commun., vol. 29, no. 2, pp. 421–430, Feb. 2011.
stitute of Technology, Pasadena, in 2008. His research interests include infor- [9] A. Avestimehr, S. Diggavi, and D. Tse, "Wireless network information mation theory, communications, and networking.
flow: A deterministic approach," IEEE Trans. Inf. Theory, vol. 57, no.
Dr. Avestimehr has received a number of awards, including the Presidential 4, pp. 1872–1905, Apr. 2011.
Early Career Award for Scientists and Engineers (PECASE) in 2011, the YoungInvestigator Program (YIP) award from the U. S. Air Force Office of Scientific [10] G. Bresler and D. Tse, "The two-user Gaussian interference channel: Research in 2011, the National Science Foundation CAREER award in 2010, A deterministic view," Eur. Trans. Telecommun., vol. 19, pp. 333–354, the David J. Sakrison Memorial Prize from the EECS Department, University of California, Berkeley, in 2008, and the Vodafone U.S. Foundation Fellows [11] A. Gamal and M. Costa, "The capacity region of a class of determin- Initiative Research Merit Award in 2005. He has been a Guest Editor for the istic interference channels," IEEE Trans. Inf. Theory, vol. 28, no. 2, pp.
IEEE TRANSACTIONS ON INFORMATION THEORY Special Issue on Interference 343–346, Mar. 1982.
[12] Z. Shao, M. Chen, A. Avestimehr, and S.-Y. Li, "Cross-layer optimiza- tion for wireless networks with deterministic channel models," IEEETrans. Inf. Theory, vol. 57, no. 9, pp. 5840–5862, Sep. 2011.
[13] H. Sato, "The capacity of the Gaussian interference channel under Suhas N. Diggavi (S'93–M'98) received the Ph.D. degree in electrical engi-
strong interference," IEEE Trans. Inf. Theory, vol. 27, no. 6, pp.
neering from Stanford University, Stanford, CA, in 1998.
786–788, Nov. 1981.
After completing the Ph.D. degree, he was a Principal Member Technical [14] S. Mohajer, S. N. Diggavi, C. Fragouli, and D. N. C. Tse, "Approx- Staff in the Information Sciences Center, AT&T Shannon Laboratories, Florham imate capacity of a class of Gaussian interference-relay networks," Park, NJ, after which he was on the faculty of the School of Computer and IEEE Trans. Inf. Theory, vol. 57, no. 5, pp. 2837–2864, May 2011.
Communication Sciences, EPFL, where he directed the Laboratory for Informa-tion and Communication Systems (LICOS). He is currently a Professor in the [15] C. Suh and D. Tse, "Feedback capacity of the Gaussian interference Department of Electrical Engineering, University of California, Los Angeles.
channel to within 2 bits," IEEE Trans. Inf. Theory, vol. 57, no. 5, pp.
His research interests include wireless communications networks, information 2667–2685, May 2011.
theory, network data compression, and network algorithms. He has eight issued [16] A. Vahid, C. Suh, and A. S. Avestimehr, "Interference channels with rate-limited feedback," IEEE Trans. Inf. Theory, 2012, to be published.
Dr. Diggavi is a recipient of the 2006 IEEE Donald Fink prize paper award, [17] V. R. Cadambe, S. A. Jafar, and C. Wang, "Interference alignment with 2005 IEEE Vehicular Technology Conference Best Paper award, and the asymmetric complex signaling—Settling the Host-Madsen—Nos- Okawa Foundation Research award. He is currently an Associate Editor for ratinia conjecture," IEEE Trans. Inf. Theory, vol. 56, no. 9, pp.
ACM/IEEE TRANSACTIONS ON NETWORKING and the IEEE TRANSACTIONS 4552–4565, Sep. 2010.
ON INFORMATION THEORY.
Gregory J. Pottie (S'84–M'89–SM'01–F'05) was born in Wilmington, DE,
and raised in Ottawa, Canada. He received the B.Sc.degree in engineering
physics from Queen's University, Kingston, Ontario, Canada, in 1984, and the
M.Eng. and Ph.D. degrees in electrical engineering from McMaster University,
Hamilton, Ontario, in 1985 and 1988, respectively.
From 1989 to 1991, he was with the Transmission Research Department of Yue Zhao (S'06–M'11) received the B.E. degree in electronic engineering from
Motorola/Codex, Canton, MA. Since 1991, he has been a faculty member of Tsinghua University, Beijing, China, in 2006, and the M.S. and Ph.D. degrees the Electrical Engineering Department, University of California, Los Angeles in electrical engineering, both from the University of California, Los Angeles (UCLA), serving in Vice-Chair roles from 1999 to 2003. From 2003 to 2009, (UCLA), Los Angeles, in 2007 and 2011, respectively.
he served as Associate Dean for Research and Physical Resources of the Henry He is currently a Postdoctoral Scholar with the Department of Electrical En- Samueli School of Engineering and Applied Science. His research interests in- gineering, Stanford University, Stanford, CA, and a Postdoctoral Research As- clude wireless communication systems and sensor networks.
sociate with the Department of Electrical Engineering, Princeton University, Dr. Pottie was secretary to the Board of Governors from 1997 to 1999 for Princeton, NJ. In summer 2010, he was a Senior Research Assistant with the the IEEE Information Theory Society. In 1998, he received the Allied Signal Department of Computer Science, City University of Hong Kong, Hong Kong.
Award for outstanding faculty research for UCLA engineering. In 2005 he be- His research interests include information theory, optimization theory and algo- came a Fellow of the IEEE for "contributions to the modeling and applications rithms, communication networks, and smart grids.
of sensor networks." In 2009, he was a Fulbright Senior Fellow at the University Dr. Zhao is a recipient of the UCLA Dissertation Year Fellowship of Sydney. He is a member of the Bruin Master's Swim Club (butterfly) and the St. Alban's Choir (second bass).

Source: http://www.cs.cityu.edu.hk/~cheewtan/ZTADP_IT.pdf