Health Articles

 

Ictopen2016_dl

> REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < Charge Density Study using Low Electrode Diameter in Epiretinal Prosthesis Diego Luján Villarreal, Dietmar Schroeder and Wolfgang H. Krautschneider. Abstract—Reducing electrode size can be advantageous for
Having as a rule of thumb that one should avoid the onset of stimulating the retina because they produce focal stimulation, i.e.
irreversible Faradaic processes when designing electrical one active electrode excites a single cell thereby greatly
stimulation systems, this would impose to keep the injected increasing resolution. The main limitation is, however, the high
charge density at a low level within reversible charge injection charge density of low electrode area that can cause adverse tissue
reactions. In this study, we analyze the use of rectangular and
linear increase pulse shapes based on charge injection capacity,
A novel strategy has been proposed [3] that generally voltage window and threshold current using a single ganglion cell
suggest keeping the pulse width narrower because it confines model with PEDOT-NaPSS arranged electrode array. We found
the amount of current that can be delivered by a stimulator, that 100µs linear increase pulse shape delivers a better response
especially if it is battery operated, and provides the minimum of charge density and electrode potential than rectangular that
charge that occurs when pulse width is of tens of µs. would avoid irreversible Faradaic reactions.

There is evidence that single linear increase pulse shape at Index Terms—charge injection capacity, linear increase pulse,
lower pulse durations can deliver lower charge than low electrode, rectangular pulse shape, retinal implant, voltage
rectangular, linear decrease and sinusoidal pulse shapes [7]. Furthermore, electrolysis of water occurs as a result when maximum cathodic and anodic potential across the electrodes surpass the "water window" boundary [8]. The water window is a potential range that is defined by the reduction of water, ETINAL prosthetic devices have strived to replace the forming hydrogen gas, in the negative direction, and the R unctionality of photoreceptors lost because of oxidation of water, forming oxygen, in the positive direction degenerative diseases such as retinitis pigmentosa (RP) or age- which may cause corrosion. related macular degeneration (AMD). These diseases are Once the electrode potential attains either of these two incurable by current treatments. Although the ability to create voltage window boundaries, all further injected charge goes visual sensations is now well established [1], the quality of into the irreversible Faradaic processes of water oxidation or vision elicited by retinal implants is facing further challenges water reduction [3]. for safely electrode implantation. PEDOT is a conductive polymer has been generated Decreasing electrode dimensions will allow focal excitation considerable attention as a supercapacitor material due to its of small groups of cells that lead to high resolution patterns of large electroactive voltage window, high chemical stability prosthetic-elicited activity and improve visual reception. This among conductive polymers [9], lower impedance and higher challenge, however, requires higher charge density that can charge injection capacity, QINJ [10]. QINJ is defined as the cause breakdown of the electrode as well as adverse tissue amount of charge per unit area that can be delivered through an electrode without causing water electrolysis. The electrochemical reactions at the electrode-tissue The aim of this study is to investigate the use of rectangular interface, i.e. capacitive double-layer charging, reversible and linear increase pulse shapes based on charge injection Faradaic and irreversible Faradaic reactions, carry out charge capacity, voltage window and threshold current using a single injection into the neural tissue [3,4,5]. The latter reaction can ganglion cell model with PEDOT-NaPSS arranged electrode produce electrolysis of water that leads to localized pH array. We give some advice on carrying out efficient changes [6], gas bubble formation that thought to be harmful stimulation by avoiding damage to the tissue and to the and physically disturbs the tissue [4, 5] and chemical species formation that damage the tissue or the electrode [3]. Manuscript received month, day, 2016; revised month, day, 2016; accepted A. Ganglion Cell Model month, day, 2016. Diego Lujan Villarreal, Dietmar Schroeder and Wolfgang H. Ganglion cell model has a basic mathematical structure for Krautschneider are with the institute of Nano and Medical Electronics at the voltage-gating based on Hodgkin and Huxley like equations Hamburg University of Technology (corresponding author phone: +49 40 [11] and is modelled with an equivalent circuit taken from 42878 3991; fax +49 40 42878 2877 previously published model of repetitive firing of retinal > REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < ganglion cells [12]. The parameters and equations that figure 1. In this work we used the identical retinal model as in describe the dynamics of the ionic channels were kept as in the The ganglion cell soma was placed inside the retina ganglion cell layer exactly below the center of active electrode B. Retinal Model and was enclosed with the cell membrane. We used the identical COMSOL model of the retina as seen In previous published works [16,17,18,19,20] there have in [13]. The model is shown in figure 1. been sufficient evidence that monophasic pulse allows the formation of Faradaic reduction reactions. If oxygen is Polyimide electrode carrier presence, these reactions may include reduction of oxygen and CROSS SECTION PLANE formation of reactive oxygen species associated in tissue Vitreous medium, VM Although monophasic is the most efficient pulse for Retina ganglion layer stimulation because of the action potential initiation and the Photoreceptor layer potential becomes insufficiently positive (using cathodic Retinal pigment epithelium pulses) where electrode corrosion may occur, however, it is not used in continuous pulses where tissue damage is to be Fig. 1. Retina model at COMSOL simulations. Layer thicknesses not drawn We used, however, monophasic rectangular and linear increase shapes with a single anodic pulse for the solely It consists of seven domains: polyimide carrier of electrodes intention to reduce the computational time consumed. PC; vitreous medium VM; retina ganglion cell layer RGC; We iterated the retinal model for each ED, IEGD and ∆t until photoreceptor layer PRC; retinal pigment epithelium RPE; we match the average boundary current density of the cell ganglion cell soma SG and the electrode array EELE. The with the extracellular threshold current amplitude obtained in ganglion cell soma was placed inside the retina ganglion cell Matlab by applying current from the active electrode. layer exactly below the center of active electrode and was We assumed that the irreversible Faradaic reactions, if enclosed with the cell membrane. present, will occur such that the charge density surpass the The material coating the electrode is PEDOT-NaPSS QINJ limit or the anodic peak potential at the electrode surpass electrodeposited in gold electrodes with a charge density of 40 the voltage window boundary. mC/cm2 as seen in [10]. The inter electrode ganglion cell distance, IEGD, are 2, 10, The electrode array configuration is shown at the cross 100 µm. The electrode diameter, ED, are 2, 10 50, 100 µm. section plane in figure 1. This arrangement is analogous to The ∆t are 50 and 100 µs. We briefly analyzed pulse duration [14,15] however it consists of an active electrode (in red) of 150 µs and yielded the highest charge density than 50 and surrounded by eight guards (in blue) in order to stress the isolation of the active electrode, to confine the stimulus Out of COMSOL simulations, we also obtained the voltage current to a small volume around the ganglion cell and to across the electrodes over time. minimize electrode cross-talk during stimulation. E. Charge Density CalculationI C. Simulation Procedure – Ganglion Cell Model (Matlab) The charge density was obtained by integrating the current In this work we used the identical ganglion cell model as in delivered by the active electrode over time and dividing it by [12] to calculate in Matlab the extracellular threshold current the electrode area. It is worth to mention that all eight density of the ganglion cell by applying monophasic surrounding electrodes including the active changed their rectangular and linear increase pulse shapes to the model at dimensions accordingly. 500 pulses per second, taking into account absolute and QINJ of gold microelectrode coated with PEDOT-NaPSS refractory period of an action potential. follows a linear relationship with charge density used during We followed the strategy as seen in [3] and we chose two electropolymerization, QD, with a constant 0.075 QINJ per QD pulse duration, ∆t, of 50 and 100 µs. Pulse widths lower than (until 300mC/cm2) for 0.001 and 1 mm2 electrode size [10]. 150 µs are analogous in [2] to directly stimulate the ganglion QINJ may also be increased by increasing electrochemical cell and to elicit solely a single spike with precise temporal surface area [21]. pattern. The peak current density amplitude was swept with a As there is no evidence about QINJ in PEDOT-NaPSS low resolution of 1 µA/cm2 until it was found the threshold current electrode area, we used the limit of 0.35 mC/cm2 for gas-free density that fires a train of action potential. and erosion-free operation [4] and 1mC/cm2 for neural The result of extracellular peak current amplitude are 330 and 120 µA/cm2 for rectangular pulse shape and 340 and 160 F. Voltage Window Boundary µA/cm2 for linear increase at 50 and 100 µs, respectively. PEDOT voltage window extends beyond conductive D. Simulation Procedure – Retinal 3D Model (COMSOL) materials, such as MnO2, from 1.5 V [23] up to 1.7 V [9]. The retinal modelling was built in COMSOL and shown in As there is no evidence about voltage window on PEDOT- > REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < NaPSS low electrode area, we used the limit of 1.7 V. B. Charge Density It is evident that the charge density, figures 2 to 4, decreases using linear increase pulse shape. A. Charge Density Results Figures 2 to 4 show the comparison of threshold charge density, left y-axis, and the threshold current for ganglion cell activation, right y-axis, for monophasic rectangular and linear increase pulse shapes. Each plot shows the results for a specific IEGD. On top of each plot the forbidden region of gas formation and neural damage are shown with a red dashed-line. Table I lists the minimum electrode diameter [µm] that can be used with their corresponding limit. The green boxes indicate the suitability to use the minimum electrode diameter tested of 2 µm. 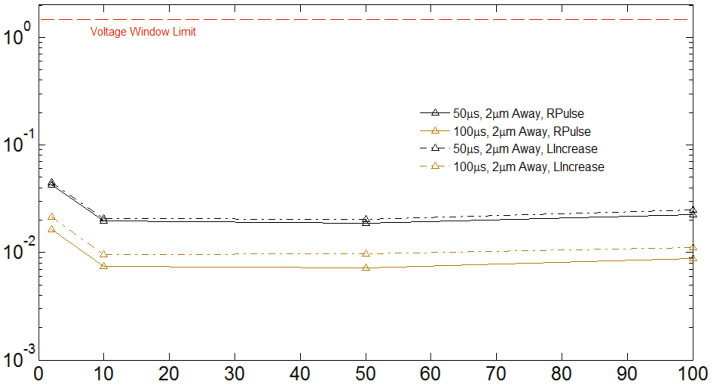Fig. 2. Threshold charge density and threshold current for 2 µm inter electrode-ganglion cell distance. HARGE DENSITY LIMITS FOR RECTANGULAR/LINEAR INCREASE PULSE Using 50 µs pulse duration, charge density is reduced up to 0.35 mC/cm2 limit 40±2.4% in average; for 100 µs, it is decreased 30±1.3%. This means a promising technique to avoid irreversible Faradaic The rectangular pulse shape has its own attributes meaning that using ED of 2 µm, 50 or 100 µs pulse duration, and IEGD lower than 10 µm is safe within the limits. This technique For a successful implant of retinal device, only the lower works with linear increase pulse shape as well. Doing so, it safe charge density of 0.35mC/cm2 should be employed. provides a method to send a more natural signal to the brain and to generate meaningful percepts. B. Voltage across Electrodes Results Figure 4 show the constraint of charge density at both limits Figures 5 and 6 illustrate the comparison of voltage across mainly when IEGD is greater than 10 µm. the electrodes. Each plot shows the results for a specific IEGD. On top of each plot the voltage window boundary is shown with a red dashed-line. Table II lists the minimum electrode diameter [µm] that can be used for the corresponding limit. VOLTAGE LIMITS FOR PULSE SHAPES Fig. 3. Threshold charge density and threshold current for 10 µm inter The green boxes indicate the suitability to use the minimum electrode-ganglion cell distance. electrode diameter tested of 2 µm. For achieving a better response in continuous pulses, charge-imbalanced biphasic waveform provides a method to A. Threshold Current reduce the irreversible charge density as reactions occurring in one phase (cathodic or anodic) are reverse in the following [3]. Threshold currents, figures 2 to 4, were found to increase Furthermore, it was demonstrated that this waveform allows with time after surgery, most likely due to the lifting off of the greater cathodic charge densities than monophasic prior to the electrode array from the retinal surface [24]. onset of tissue damage [26]. Threshold variations with respect to IEGD are consistent with previous experimental work of epiretinal device implanted in C. Voltage across Electrodes It is also evident that using 100 µs pulse duration, more than Because linear increase shape injects less charge than one third but less than half of electrode voltage, fig. 5 and 6, is rectangular for a given pulse duration, the former necessitates reduced than 50 µs for both pulse shapes. This technique a higher amplitude to reach threshold. would avoid irreversible Faradaic reactions.

> REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < For attaining a better response in successive pulses, the charge-imbalanced waveform has advantages in avoiding corrosion by decreasing the maximum positive potential since the anodic phase is no longer constrained to be equal to the cathodic phase as charge-balanced pulse, thus the electrode potential reaches less positive values [3,26]. We found that 100µs linear increase pulse shape delivers a better response of charge density and electrode potential than rectangular that would avoid irreversible Faradaic reactions. Fig. 4. Threshold charge density and threshold current for 100 µm inter Furthermore, for a given IEGD with charge density limit of electrode-ganglion cell distance. 0.35mC/cm2 and voltage window limit of 1.7V, our model Considering figure 5 and 6, we learn that it is safe to work i) 0<IEGD<10 µm: a) reduce electrode diameter to 2 µm; b) work with either 50 or 100 µs low pulse duration; c) use either D of 2 µ m, low pulse durations lower than 150 µ s, IEGD lower than 10 µm with either rectangular or linear increase rectangular or linear increase pulse shapes. ii) 10<IEGD<100 µm (for rectangular pulse): a) reduce electrode diameter to 14 µm only with 100 µs pulse duration. For 50 µs, electrode diameter should be 18 µm. iii) 10<IEGD<100 µm (for linear increase pulse): a) reduce electrode diameter to 10 µm with either 50 or 100 µs pulse duration. If pulse trains are needed, the charge-imbalanced waveform has added advantages in avoiding corrosion and reducing irreversible charge densities that leads to either electrode or tissue damage [3,26]. Additional experimental testing of small electrodes is still required to verify our results. Moreover, further simulations of heat dissipation should be performed to verify the use of Fig. 5. Voltage results for 2 µm inter electrode-ganglion cell distance for 1000+ electrode array for epi- or subretinal implants. rectangular and linear increase pulse shapes. Figure 6 show that the constraint of voltage window limit [1] Cai, Qiushi, et al. Response variability to high rates of electric originates mainly when IEGD is greater than 10 µm. stimulation in retinal ganglion cells. J Neurophysiology, 2011. [2] Fried S., et al. A Method for Generating Precise Temporal Patterns of Retinal Spiking Using Prosthetic Stimulation. J Neurophysiol 95: 970–978, 2006. [3] D. R. Merrill, M. Bikson, and J. G. Jefferys, "Electrical stimulation of excitable tissue: Design of efficacious and safe protocols,"J. Neurosci. Methods , vol. 141, no. 2, pp. 171–198, Feb. 15, 2005. [4] S. B. Brummer and M. J. Turner, "Electrochemical considerations for safe electrical stimulation of the nervous system with platinum electrodes," IEEE Trans. Biomed. Eng., vol. 24, no. 1, pp. 59–63, Jan. 1977. [5] S. F. Cogan, "Neural stimulation and recording electrodes," Annu. Rev. Biomed. Eng., vol. 10, pp. 275–309, 2008. [6] C. Q. Huang, P. M. Carter, and R. K. Shepherd, "Stimulus induced pH changes in cochlear implants: An in vitro and in vivo study," Ann. Biomed. Eng., vol. 29, no. 9, pp. 791–802, Sep. 2001. [7] Mario A. Meza-Cuevas, Dietmar Schroeder and Wolfgang H. Fig. 6. Voltage results for 10 and 100 µm inter electrode-ganglion cell Krautschneider. Neuromuscular Electrical Stimulation Using Different distance for rectangular and linear increase pulse shapes. Waveforms - Properties comparison by applying single pulses. 5th International Conference on BioMedical Engineering and Informatics, It should be noted that in fact irreversible processes might occur at potentials within the voltage window, such as [8] Ronald T. Leung, Mohit N. Shivdasani, David A. X. Nayagam, Robert K. Shepherd. In Vivo and In Vitro Comparison of the Charge Injection irreversible oxygen reduction, as opposed to the opinion in Capacity of Platinum Macroelectrodes. IEEE Transactions on many studies that states reversible charge storage capacity, or Biomedical Engineering, Vol. 62, No. 3, March 2015. [9] Jonathon Duay, Eleanor Gillette, Ran Liu, Sang Bok Lee. Highly INJ, can be applied without the electrode potential exceeds flexible pseudocapacitor based on freestanding heterogeneous the voltage window during pulsing [3]. Therefore, QINJ and MnO2/conductive polymer nanowire arrays. Phys. Chem. Chem. Phys., voltage window limits need to be analyzed separately. 2012, 14, 3329–3337. > REPLACE THIS LINE WITH YOUR PAPER IDENTIFICATION NUMBER (DOUBLE-CLICK HERE TO EDIT) < [10] Starbird, R. et al. Electrochemical properties of PEDOT-NaPSS He has worked with the Cellular Therapy galvanostatically deposited from an aqueous micellar media for invasive Department in the School of Medicine at electrodes, IEEE BMEICON, 2012. [11] Hodgkin A., et al. A quantitative description of membrane current and ITESM, Monterrey, México, and he is its application to conduction and excitation in nerve. J. Physiol, 1952. now pursuing his PhD in the Institute of [12] Fohlmeister J., et al. Modeling the repetitive firing of retinal ganglion Nano and Medical Electronics at the cells. Brain Research, 1989. Hamburg University of Technology, [13] Lujan Villarreal D., et al. "Feasibility Study of a 1000+ Electrode Array in Epiretinal Prosthesis." (Forthcoming, 2016) 8th International Hamburg, Germany. Conference on Bioinformatics and Biomedical Technology. Barcelona, His main research interests focus on Spain. June 10-12, 2016. theoretical models of neurostimulation, optimal energy-saving [14] Lovell N., et al. Current distribution during parallel stimulation: algorithms and epi- and sub retinal stimulation. Implications for an epiretinal neuroprosthesis. IEEE Eng Med Biol Soc, [15] Dommel N., et al. A CMOS retinal neurostimulator capable of focussed, simultaneous stimulation J Neural Eng, vol. 6, pp. 035006, 2009. [16] Halliwell B. Reactive oxygen species and the central nervous system. J Neurochem 1992;59(5):1609–23. Schroeder
[17] Imlay JA. Pathways of oxidative damage. Annu Rev Microbiol 2003;57:395–418. received the Dr. Ing. degree in electrical [18] Bergamini CM, Gambetti S, Dondi A, Cervellati C. Oxygen, reactive oxygen species and tissue damage. Curr Pharm Des 2004;10(14):1611– Universität Braunschweig, Braunschweig, Germany, in 1984. [19] Stohs SJ. The role of free radicals in toxicity and disease. J Basic Clin Physiol Pharmacol 1995;6(3–4):205–28. He joined the Hamburg University of [20] Hemnani T, Parihar MS. Reactive oxygen species and oxidative DNA Technology, Hamburg, Germany, in damage. Indian J Physiol Pharmacol 1998;42(4):440–52. 1983, where he has been a Lecturer with [21] Mario A. Meza-Cuevas. Stimulation of Neurons by Electrical Means. Semiconductor Electronics since 1994. Logos Verlag Berlin GmbH. 2015. [22] Warren E. Finn, et al. Handbook of Neuroprosthetic Methods. CRC Press, Dec 16, 2002. [23] Boretius, T., M. Schuettler, and T. Stieglitz. On the Stability of PEDOT as Coating Material for Active Neural Implants. 15th Annual Conference of the International Functional Electrical Stimulation Society, 2010. Wolfgang H. Krautschneider (M'85)
[24] Chader G., et al. Artificial vision: needs, functioning, and testing of retinal electronic prosthesis. Progress Brain Research, Vol. 175, 2009. Habilitation degrees from the Berlin [25] Jensen R., et al. Thresholds for Activation of Rabbit Retinal Ganglion Cells with Relatively Large, Extracellular Microelectrodes. IOVS, 2005. [26] Scheiner A, Mortimer JT. Imbalanced biphasic electrical stimulation: muscle tissue damage. Ann Biomed Eng 1990. Laboratories, IBM, Yorktown Heights, Diego Lujan Villarreal was born in Monterrey, Nuevo León,
NY, USA, the Siemens Research Center, México in 1983. He received the B.S. degree in Mechatronics Munich, Germany, and the DRAM from the Monterrey Institute of Technology and Higher Project of IBM and Siemens, Essex Junction, VT, USA. Education (ITESM) in 2006 and the M.S. degree in He is currently the Head of the Institute of Nano and Medical Microelectronics and Microsystems from the Hamburg Electronics at the Hamburg University of Technology, University of Technology in 2010. Hamburg, Germany.

Source: http://www.ictopen.nl/binaries/content/assets/bestanden/ict-open-2016/proceedings/villarreal-diego-lujan.pdf